Clustered matrix approximations, with randomized algorithms: Test 3
Symmetric matrix A, with dense diagonal block structure
Contents
Load data
clear % Load partial LiveJournal data load('lj-partial')
Clustering with GRACLUS
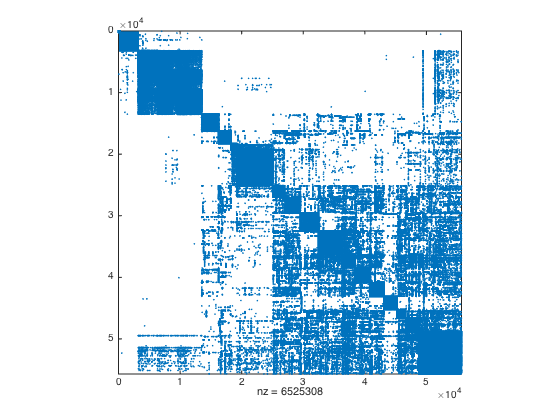
% Number of clusters noc = 20; [prt,obj] = graclus(A,noc); % Reorder vertices [ind,prtsz,prtc] = reorderVertices(prt); % Visualize clustering structure of A spy(A(ind,ind))
---------------------------------------------------------------------- Graclus 1.2 Copyright 2008, Brian Kulis and Yuqiang Guan Graph Information: #Vertices: 55692, #Edges: 3262654, #Clusters: 20 #local search steps: 0 Normalized-Cut... Cut value: 0.874304, Balance: 2.49 Timing Information: I/O: 0.034 Clustering: 1.143 (Graclus time) Total: 1.195 ----------------------------------------------------------------------
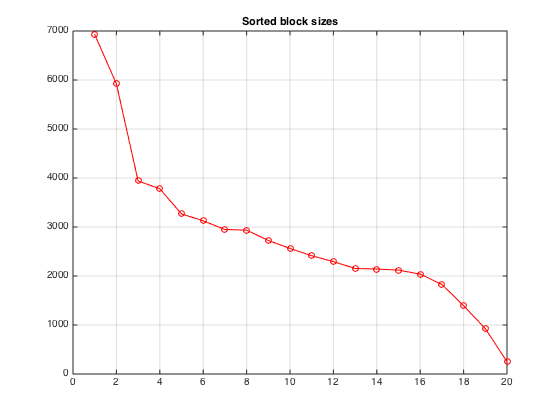
Plot sorted block sizes
% sort and plot block sizes ssz = sort(prtsz,'descend'); plot(ssz,'r-o') title('Sorted block sizes') grid on
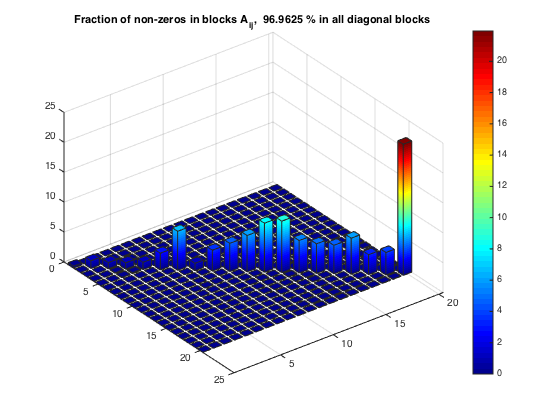
Fraction of non-zeros within diagonal blocks
[nnzBlks, nnzBlFr, nnzFrac] = compClustNnz(A,prtc); bar3custom(nnzBlFr) title(['Fraction of non-zeros in blocks A_{ij}, ', num2str(nnzFrac), ... ' % in all diagonal blocks']) % Relative error due to clustering: || A - diag(A11,...,Acc) || / || A || relerr = compClustRelErr(A,prtc); fprintf('Fraction of non-zeros in diagonal blocks : %8.2f %% \n', nnzFrac) fprintf('Relative error in a block diagonal approx.: %8.2f %% \n', relerr)
Fraction of non-zeros in diagonal blocks : 96.96 % Relative error in a block diagonal approx.: 17.43 %
Compute clustered matrix approximatons with randomized algorithms
% Specify rank k for approximations of diagonal blocks k = 20; % Or use different ranks for different blocks %k = [2,3,4,5,6,2,3,4,5,6,2,3,4,5,6,2,3,4,5,6]'; % Specify oversampling and power parameters p and q, respectively p = 1; q = 2; % Compute approximations for diagonal blocks of a symmetric matrix [Vra, Dra] = clustRandAlg(A,prtc,k,p,'sym'); [Vrap,Drap] = clustRandAlgPow(A,prtc,k,p,q,'sym'); [V,D] = clustEigs(A,prtc,k,'eigs'); % Compute core matrix % Compute the core matrix to get an approximation of entire A, i.e. % A \approx V*DD*V' DDra = compCoreSymFull(A,Vra, [],prtc,'dense'); DDrap = compCoreSymFull(A,Vrap,[],prtc,'dense'); DD = compCoreSymFull(A,V,D,prtc,'diag');
Compute relative errors in % of clustered matrix approximations
nA = norm(A,'fro'); relerrCmappRA = sqrt( nA^2 - norm(DDra, 'fro')^2 )/nA*100; relerrCmappRAP = sqrt( nA^2 - norm(DDrap,'fro')^2 )/nA*100; relerrCmappEigs = sqrt( nA^2 - norm(DD,'fro')^2 )/nA*100; % Compute memory consumption memCmapp = memUsageCmapp(Vra,DDra,[],'sym'); % Get rank k for a regular matrix approximation with = or > memory usage m = size(A,1); [memRmapp3,kreg] = memUsageRmapp(m,[],memCmapp,'sym'); Vr1 = randAlg(A,kreg,p,'orth'); Vr2 = randAlgPow(A,kreg,p,q,'orth'); [Vr3,Dr3] = eigs(A,kreg); Dr1 = Vr1'*A*Vr1; Dr2 = Vr2'*A*Vr2; relerrRmappRA = sqrt( nA^2 - norm(Dr1,'fro')^2 )/nA*100; relerrRmappRAP = sqrt( nA^2 - norm(Dr2,'fro')^2 )/nA*100; relerrRmappEigs = sqrt( nA^2 - norm(Dr3,'fro')^2 )/nA*100; % fpns = floating point numbers disp('-------------------------------------------------------------------') fprintf('Clustered matrix approximation with randAlg : relErr = %10.2f %% \n', relerrCmappRA) fprintf('Clustered matrix approximation with randAlgPow: relErr = %10.2f %% \n', relerrCmappRAP) fprintf('Clustered matrix approximation with Eigs : relErr = %10.2f %% \n', relerrCmappEigs) fprintf('Regular matrix approximation with randAlg : relErr = %10.2f %% \n', relerrRmappRA) fprintf('Regular matrix approximation with randAlgPow: relErr = %10.2f %% \n', relerrRmappRAP) fprintf('Regular matrix approximation with eigs : relErr = %10.2f %% \n', relerrRmappEigs) disp('-------------------------------------------------------------------') fprintf('Clustered matrix approximation: memUsage = %10.0f fpns \n', memCmapp) fprintf('Regular matrix approximation: memUsage = %10.0f fpns \n', memRmapp3) disp('-------------------------------------------------------------------')
------------------------------------------------------------------- Clustered matrix approximation with randAlg : relErr = 73.14 % Clustered matrix approximation with randAlgPow: relErr = 53.57 % Clustered matrix approximation with Eigs : relErr = 52.31 % Regular matrix approximation with randAlg : relErr = 93.98 % Regular matrix approximation with randAlgPow: relErr = 78.78 % Regular matrix approximation with eigs : relErr = 77.97 % ------------------------------------------------------------------- Clustered matrix approximation: memUsage = 1257522 fpns Regular matrix approximation: memUsage = 1280939 fpns -------------------------------------------------------------------
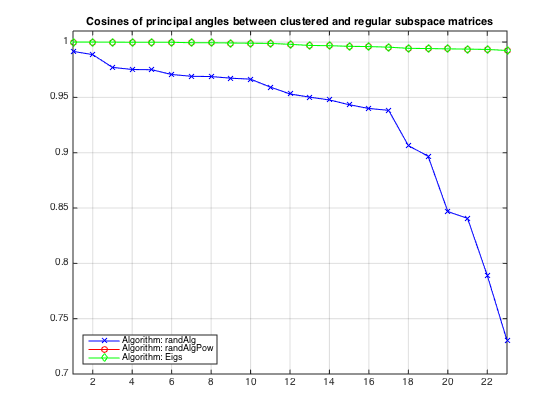
Compute cosines of principal angles
% Compute angles for column space matrices angRA = compSubspaceAngles(Vr3,Vra,prtc); angRAP = compSubspaceAngles(Vr3,Vrap,prtc); angEigs = compSubspaceAngles(Vr3,V,prtc); clf plot(angRA,'b-x') hold on plot(angRAP,'r-o') plot(angEigs,'g-d') grid on title('Cosines of principal angles between clustered and regular subspace matrices') legend('Algorithm: randAlg','Algorithm: randAlgPow', 'Algorithm: Eigs','location','SouthWest') xlim([1,kreg]) ylim([0.7,1.01])