Clustered matrix approximations: Test 4
Rectangular matrix A, with dense diagonal block structure
Contents
Load data
clear % Load processed NotreDame data load('NotreDame_actors_preprocessed')
Clustering with GRACLUS
% Number of clusters noc = 20; [m,n] = size(A); B = [sparse(m,m) A; A' sparse(n,n)]; [prt,obj] = graclus(B,noc); clear B % Extract row and column vertices, then reorder rprt = prt(1:m); cprt = prt(m+1:end); [rind,rprtsz,rprtc] = reorderVertices(rprt); [cind,cprtsz,cprtc] = reorderVertices(cprt); % Visualize clustering structure of A spy(A(rind,cind))
---------------------------------------------------------------------- Graclus 1.2 Copyright 2008, Brian Kulis and Yuqiang Guan Graph Information: #Vertices: 175826, #Edges: 1016127, #Clusters: 20 #local search steps: 0 Normalized-Cut... Cut value: 2.426337, Balance: 4.43 Timing Information: I/O: 0.011 Clustering: 1.963 (Graclus time) Total: 1.989 ----------------------------------------------------------------------

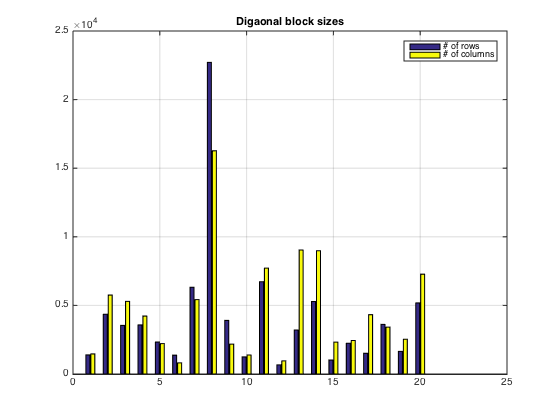
Plot of diagonal block sizes
bar([rprtsz cprtsz]) title('Digaonal block sizes') grid on legend('# of rows','# of columns')
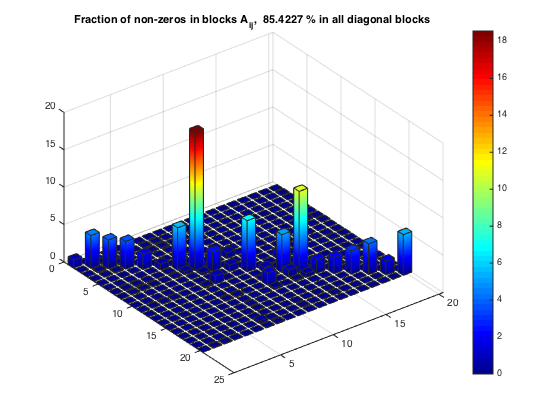
Fraction of non-zeros within diagonal blocks
[nnzBlks, nnzBlFr] = compClustNnzRect(A,rprtc,cprtc); nnzFrac = sum(diag(nnzBlks))/nnz(A)*100; bar3custom(nnzBlFr) title(['Fraction of non-zeros in blocks A_{ij}, ', num2str(nnzFrac), ... ' % in all diagonal blocks']) % Relative error due to clustering: || A - diag(A11,...,Acc) || / || A || msk = logical(eye(noc)); relerr = compClustRelErrExt(A,rprtc,cprtc,msk); fprintf('Fraction of non-zeros in diagonal blocks : %8.2f %% \n', nnzFrac) fprintf('Relative error in a block diagonal approx.: %8.2f %% \n', relerr)
Fraction of non-zeros in diagonal blocks : 85.42 % Relative error in a block diagonal approx.: 38.18 %
Compute clustered matrix approximatons
% Specify rank k for approximations of diagonal blocks % Or use different ranks for different blocks k = 30; % Compute approximations for diagonal blocks of a rectangular matrix [U,S,V] = clustSvdsRectDiag(A,rprtc,cprtc,k,'svds'); % if lansvd is available and prefered %[U,S,V] = clustSvdsRectDiag(A,rprtc,cprtc,k,'lansvd'); SS = compCoreNonsymCell(A,U,S,V,rprtc,cprtc,'diag'); SS = cell2mat(SS);
Compute relative error in % of clustered matrix approximation
nA = norm(A,'fro'); relerrCmapp = sqrt( nA^2 - norm(SS,'fro')^2 )/nA*100; % Compute memory consumption memCmapp = memUsageCmapp(U,SS,V,'non-sym'); % Get rank k for a regular matrix approximation with = or > memory usage [m,n] = size(A); [memRmapp,kreg] = memUsageRmapp(m,n,memCmapp,'sym'); [Ur,Sr,Vr] = svds(A,kreg); relerrRmapp = sqrt( nA^2 - norm(Sr,'fro')^2 )/nA*100; % fpns = floating point numbers disp('-------------------------------------------------------------------') fprintf('Clustered matrix approximation: relErr = %10.2f %% \n', relerrCmapp) fprintf('Regular matrix approximation: relErr = %10.2f %% \n', relerrRmapp) disp('-------------------------------------------------------------------') fprintf('Clustered matrix approximation: memUsage = %10.0f fpns \n', memCmapp) fprintf('Regular matrix approximation: memUsage = %10.0f fpns \n', memRmapp) disp('-------------------------------------------------------------------')
------------------------------------------------------------------- Clustered matrix approximation: relErr = 95.62 % Regular matrix approximation: relErr = 98.48 % ------------------------------------------------------------------- Clustered matrix approximation: memUsage = 5634780 fpns Regular matrix approximation: memUsage = 5645856 fpns -------------------------------------------------------------------