Clustered matrix approximations: Test 5

Rectangular matrix A, with dense non-diagonal block structure

Contents

Load data

clear
% load processed NotreDame data
load('NotreDame_actors_preprocessed')

Clustering with GRACLUS

% max cluster size
maxClustSize = 12000;
[m,n] = size(A);
B  = [sparse(m,m) A; A' sparse(n,n)];

% load partitioning result to suppress graclus outputs for publish purposes
%[prt,obj] = recGraclus(B,maxClustSize);
load test5var
clear B
% Reorder vertices
rprt = prt(1:m);
cprt = prt(m+1:end);

[rind,rprtsz,rprtc] = reorderVertices(rprt);
[cind,cprtsz,cprtc] = reorderVertices(cprt);

% Visualize clustering structure of A
spy(A(rind,cind))

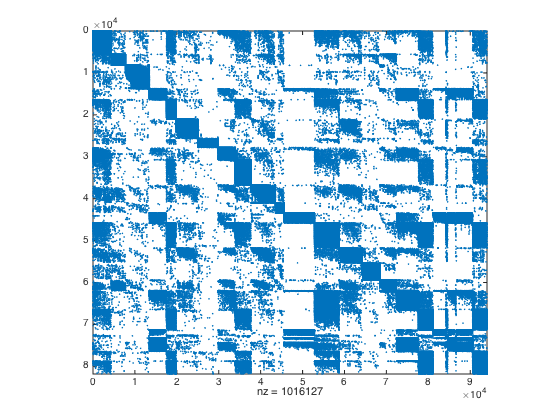
Determine and visualise location of dense blocks

threshold = 0.15;
[msk,~,totFrc] = determineDenseBlocks(A,rprtc,cprtc,threshold);
clf
spy(msk)
nDenseBlocks = nnz(msk);

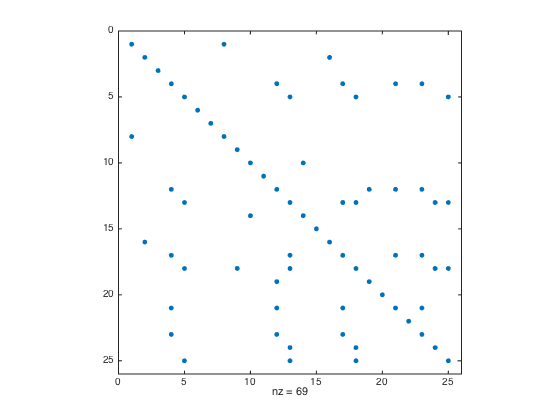
Fraction of non-zeros within diagonal blocks

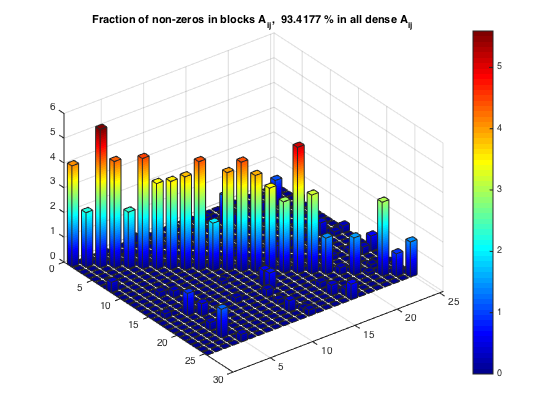
[nnzBlks, nnzBlFr] = compClustNnzRect(A,rprtc,cprtc);

bar3custom(msk.*nnzBlFr)
title(['Fraction of non-zeros in blocks A_{ij},  ', num2str(totFrc), ...
    ' % in all dense A_{ij}'])

% Relative error due to clustering: || A - A_dense || / || A ||
% where A_dense only contains non-zeros from dense blocks.
relerr = compClustRelErrExt(A,rprtc,cprtc,msk);
fprintf('Fraction of non-zeros in dense blocks     : %8.2f %% \n', totFrc)
fprintf('Relative error in a block diagonal approx.: %8.2f %% \n', relerr)

Fraction of non-zeros in dense blocks     :    93.42 % 
Relative error in a block diagonal approx.:    25.66 % 

Compute clustered matrix approximatons

% Specify rank k for approximations of dense blocks
% Or use different ranks for different blocks
k = 20;
K = (ones(size(msk))*k).*msk;
% Compute approximations for dense blocks of a rectangular matrix
[U,S,V] = clustSvdsRect(A,K,rprtc,cprtc,'svds');

% if lansvd is available and prefered
%[U,S,V] = clustSvdsRect(A,rprtc,cprtc,k,'lansvd');

% Specify parameters for clustered randomized algorithms
p = 2;
P = (ones(size(msk))*p).*msk;
q = 2;
Q = (ones(size(msk))*q).*msk;
[Ur,Sr,Vr] = clustRandAlgRect(A,K,P,Q,rprtc,cprtc);

SS  = cell2mat(S);
SSr = cell2mat(Sr);

Compute relative error in % of clustered matrix approximation

nA  = norm(A,'fro');
relerrCmapp  = sqrt( nA^2 - norm(SS, 'fro')^2 )/nA*100;
relerrCmappR = sqrt( nA^2 - norm(SSr,'fro')^2 )/nA*100;

% Compute memory consumption
memCmapp  = memUsageCmapp(U,SS,V,'non-sym');
memCmappR = memUsageCmapp(Ur,SSr,Vr,'non-sym');

% Get rank k for a regular matrix approximation with = or > memory usage
[m,n] = size(A);
[memRmapp,kreg] = memUsageRmapp(m,n,memCmapp,'sym');

[Ur,Sr,Vr] = svds(A,kreg);
relerrRmapp = sqrt( nA^2 - norm(Sr,'fro')^2 )/nA*100;

% fpns = floating point numbers
disp('-------------------------------------------------------------------')
fprintf('Clustered matrix approximation: relErr    = %10.2f %% \n', relerrCmapp)
fprintf('Clustered matrix approximation: relErr    = %10.2f %%  (randomized) \n', relerrCmappR)
fprintf('Regular   matrix approximation: relErr    = %10.2f %% \n', relerrRmapp)
disp('-------------------------------------------------------------------')
fprintf('Clustered matrix approximation: memUsage  = %10.0f fpns \n', memCmapp)
fprintf('Clustered matrix approximation: memUsage  = %10.0f fpns (randomized) \n', memCmappR)
fprintf('Regular   matrix approximation: memUsage  = %10.0f fpns \n', memRmapp)
disp('-------------------------------------------------------------------')

-------------------------------------------------------------------
Clustered matrix approximation: relErr    =      94.85 % 
Clustered matrix approximation: relErr    =      95.08 %  (randomized) 
Regular   matrix approximation: relErr    =      97.51 % 
-------------------------------------------------------------------
Clustered matrix approximation: memUsage  =   12065020 fpns 
Clustered matrix approximation: memUsage  =   13481006 fpns (randomized) 
Regular   matrix approximation: memUsage  =   12109952 fpns 
-------------------------------------------------------------------

Published with MATLAB® R2014b