Clustered matrix approximations: Test 6

Rectangular matrix A, with dense non-diagonal block structure, and independent row and column clustering

Contents

Load data

clear
% Load processed NotreDame data
load NotreDame_actors_preprocessed
[m,n] = size(A);

Cluster rows of a rectangular matrix (bipartite graph)

% Normalize rows of A
B = normalizeColumns(A')';
B = B*B';

% Determine threshold value
%[rr,cc,vv] = find(B);
%semilogy(sort(vv,'descend'))
%grid on

% Threshold matrix and cluster with GRACLUS
B = matrixThreshold(B,0.1);
rnoc = 15;
[rprt,~] = graclus(B,rnoc);
[rind,rprtsz,rprtc] = reorderVertices(rprt);

----------------------------------------------------------------------
 Graclus 1.2 Copyright 2008, Brian Kulis and Yuqiang Guan 

Graph Information:
  #Vertices: 81823, #Edges: 1836035, #Clusters: 15
#local search steps: 0

Normalized-Cut... 
   Cut value: 2.434641, Balance:  1.39 

Timing Information:
  I/O:          		   0.018
  Clustering:   		   4.405   (Graclus time)
  Total:        		   4.449
----------------------------------------------------------------------

Cluster columns of a rectangular matrix (bipartite graph)

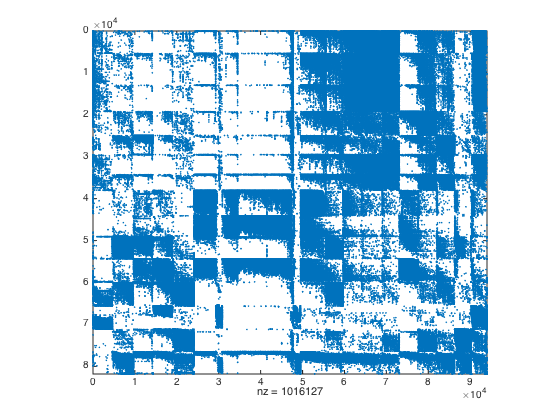
% Normalize columns of A
B = normalizeColumns(A);
B = B'*B;

% Determine threshold value
%[rr,cc,vv] = find(B);
%semilogy(sort(vv,'descend'))
%grid on

% Threshold matrix and cluster with GRACLUS
B = matrixThreshold(B,0.1);
cnoc = 20;
[cprt,~] = graclus(B,cnoc);
[cind,cprtsz,cprtc] = reorderVertices(cprt);
spy(A(rind,cind))

----------------------------------------------------------------------
 Graclus 1.2 Copyright 2008, Brian Kulis and Yuqiang Guan 

Graph Information:
  #Vertices: 94003, #Edges: 6926728, #Clusters: 20
#local search steps: 0

Normalized-Cut... 
   Cut value: 4.299469, Balance:  2.84 

Timing Information:
  I/O:          		   0.068
  Clustering:   		  15.295   (Graclus time)
  Total:        		  15.437
----------------------------------------------------------------------

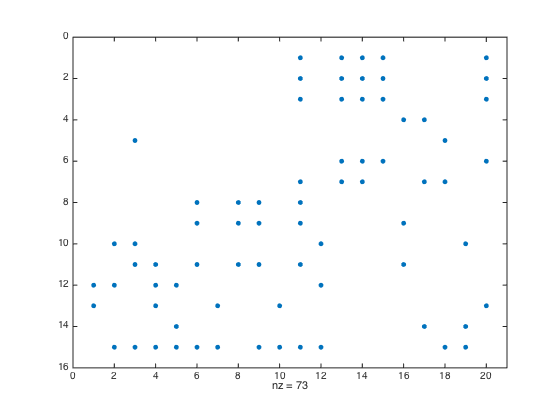
Determine dense blocks

threshold = 0.25;
[msk,~,totFrc] = determineDenseBlocks(A,rprtc,cprtc,threshold);
clf
spy(msk)
nDenseBlocks = nnz(msk);
disp(['Total number of dense blocks: ', int2str(sum(sum(msk))), ' of ',...
    int2str(rnoc*cnoc)])

Total number of dense blocks: 73 of 300

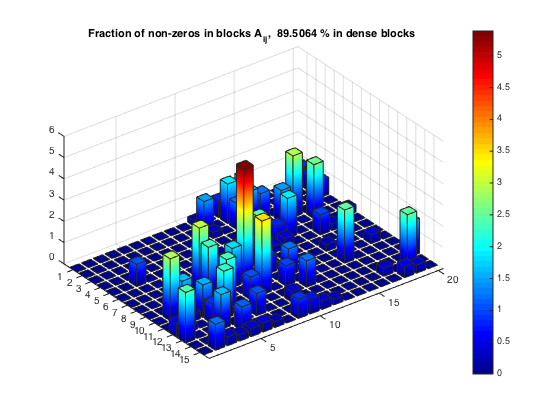
Fraction of non-zeros within dense blocks

[nnzBlks, nnzBlFr] = compClustNnzRect(A,rprtc,cprtc);
bar3custom(msk.*nnzBlFr)
title(['Fraction of non-zeros in blocks A_{ij},  ', num2str(totFrc), ...
    ' % in dense blocks '])

Compute clustered matrix approximatons

% Specify rank k for approximations of dense blocks
% Or use different ranks for different blocks
k = 15;
K = (ones(size(msk))*k).*msk;
% Compute approximations of dense blocks of a rectangular matrix
[U,S,V] = clustSvdsRect(A,K,rprtc,cprtc,'svds');

% if lansvd is available and prefered
%[U,S,V] = clustSvdsRect(A,rprtc,cprtc,k,'lansvd');

% Specify parameters for clustered randomized algorithms
p = 2;
P = (ones(size(msk))*p).*msk;
q = 2;
Q = (ones(size(msk))*q).*msk;
[Ur,Sr,Vr] = clustRandAlgRect(A,K,P,Q,rprtc,cprtc);

SS  = cell2mat(S);
SSr = cell2mat(Sr);

Compute relative error in % of clustered matrix approximation

nA  = norm(A,'fro');
relerrCmapp  = sqrt( nA^2 - norm(SS, 'fro')^2 )/nA*100;
relerrCmappR = sqrt( nA^2 - norm(SSr,'fro')^2 )/nA*100;

% Compute memory consumption
memCmapp  = memUsageCmapp(U,SS,V,'non-sym');
memCmappR = memUsageCmapp(Ur,SSr,Vr,'non-sym');

% Get rank k for a regular matrix approximation with the same memory usage
[m,n] = size(A);
[memRmapp,kreg] = memUsageRmapp(m,n,memCmapp,'sym');


[Us,Ss,Vs] = svds(A,kreg);
relerrRmapp = sqrt( nA^2 - norm(Ss,'fro')^2 )/nA*100;

% fpns = floating point numbers
disp('-------------------------------------------------------------------')
fprintf('Clustered matrix approximation: relErr    = %10.2f %% \n', relerrCmapp)
fprintf('Clustered matrix approximation: relErr    = %10.2f %%  (randomized) \n', relerrCmappR)
fprintf('Regular   matrix approximation: relErr    = %10.2f %% \n', relerrRmapp)
disp('-------------------------------------------------------------------')
fprintf('Clustered matrix approximation: memUsage  = %10.0f fpns \n', memCmapp)
fprintf('Clustered matrix approximation: memUsage  = %10.0f fpns (randomized) \n', memCmappR)
fprintf('Regular   matrix approximation: memUsage  = %10.0f fpns \n', memRmapp)
disp('-------------------------------------------------------------------')

-------------------------------------------------------------------
Clustered matrix approximation: relErr    =      94.50 % 
Clustered matrix approximation: relErr    =      94.65 %  (randomized) 
Regular   matrix approximation: relErr    =      97.43 % 
-------------------------------------------------------------------
Clustered matrix approximation: memUsage  =   12637035 fpns 
Clustered matrix approximation: memUsage  =   14503159 fpns (randomized) 
Regular   matrix approximation: memUsage  =   12682720 fpns 
-------------------------------------------------------------------

Compute cosines of principal angles

% Compute angles for column space matrices
angCol = compSubspaceAngles(Us,U,rprtc);

% Compute angles for row space matrices
angRow = compSubspaceAngles(Vs,V,cprtc);

plot(angCol)
hold on
plot(angRow)
grid on
hold off
title('Cosines of principal angles between clustered and regular subspace matrices')
legend('Column space matrices','Row space matrices','location','SouthWest')
xlim([1,kreg])

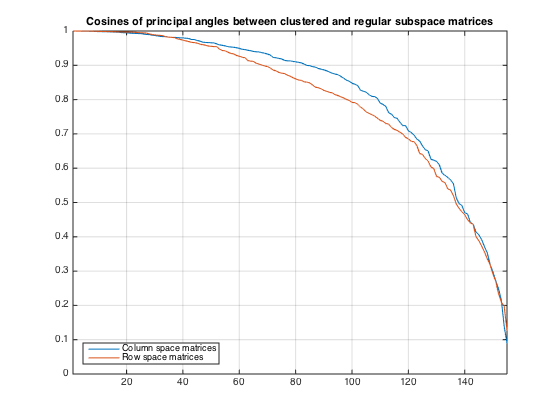
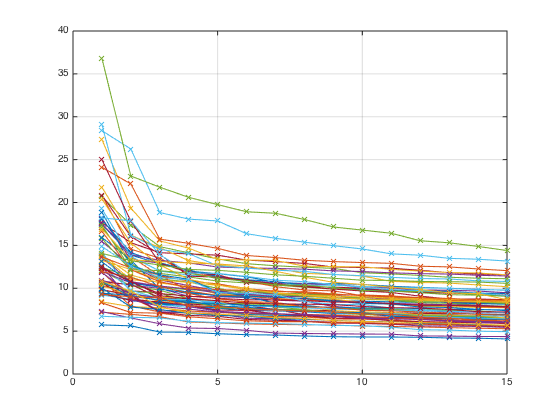
Compute SVDs of all dense blocks

[UU,SS,VV] = clustSvdsExtRectCell(A,K,rprtc,cprtc,'svds');

% Plot singular values for dense blocks
clf
for i = 1:rnoc
    for j = 1:cnoc
        if K(i,j) > 0
           plot(diag(SS{i,j}),'-x');
           hold on
        end
    end
end
grid on
hold off

Published with MATLAB® R2014b